Neuron Collections#
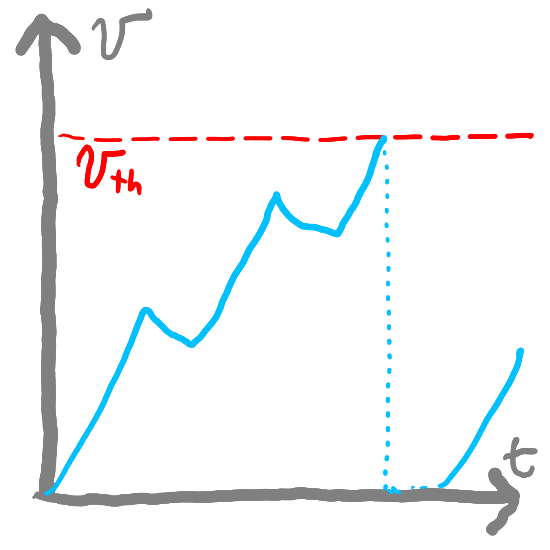
Our classes for LIF neurons and synapses currently represent one neuron or synapse. However, we usually want to represent many neurons and synapses. We could do this by creating many instances of the Neuron class but this would be inefficient. Instead, we can create a NeuronCollection class that can store many neurons and update them in parallel.
What does “in parallel” mean?
Suppose we have a list L and want to multiply each element by 1.2. We could do this in a loop:
L = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# Update L by multiplying each element by 1.2
for i in range(len(L)): # i is the index of the element (0, 1, 2, ...)
L[i] = L[i] * 1.2
This is called updating the list sequentially; we loop over the sequence and update each item in L one-by-one. We could instead do this in parallell, meaning that we will update every item at the same time:
import numpy as np
L = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
L = L * 1.2 # Multiply each element by 1.2 in parallel
If we use NumPy, we can update our old code to represent groups of neurons:
Show code cell source
import numpy as np
np.random.seed(0)
class LIFCollection:
def __init__(self, n=1, dim=1, tau_rc=0.02, tau_ref=0.002, v_th=1,
max_rates=[200, 400], intercept_range=[-1, 1], t_step=0.001, v_init = 0):
self.n = n
# Set neuron parameters
self.dim = dim # Dimensionality of the input
self.tau_rc = tau_rc # Membrane time constant
self.tau_ref = tau_ref # Refractory period
self.v_th = np.ones(n) * v_th # Threshold voltage for spiking
self.t_step = t_step # Time step for simulation
# Initialize state variables
self.voltage = np.ones(n) * v_init # Initial voltage of neurons
self.refractory_time = np.zeros(n) # Time remaining in refractory period
self.output = np.zeros(n) # Output spikes
# Generate random max rates and intercepts within the given range
max_rates_tensor = np.random.uniform(max_rates[0], max_rates[1], n)
intercepts_tensor = np.random.uniform(intercept_range[0], intercept_range[1], n)
# Calculate gain and bias for each neuron
self.gain = self.v_th * (1 - 1 / (1 - np.exp((self.tau_ref - 1/max_rates_tensor) / self.tau_rc))) / (intercepts_tensor - 1)
self.bias = np.expand_dims(self.v_th - self.gain * intercepts_tensor, axis=1)
# Initialize random encoders
self.encoders = np.random.randn(n, self.dim)
self.encoders /= np.linalg.norm(self.encoders, axis=1)[:, np.newaxis]
def reset(self):
# Reset the state variables to initial conditions
self.voltage = np.zeros(self.n)
self.refractory_time = np.zeros(self.n)
self.output = np.zeros(self.n)
def step(self, inputs):
dt = self.t_step # Time step
# Update refractory time
self.refractory_time -= dt
delta_t = np.clip(dt - self.refractory_time, 0, dt) # ensure between 0 and dt
# Calculate input current
I = np.sum(self.bias + inputs * self.encoders * self.gain[:, np.newaxis], axis=1)
# Update membrane potential
self.voltage = I + (self.voltage - I) * np.exp(-delta_t / self.tau_rc)
# Determine which neurons spike
spike_mask = self.voltage > self.v_th
self.output[:] = spike_mask / dt # Record spikes in output
# Calculate the time of the spike
t_spike = self.tau_rc * np.log((self.voltage[spike_mask] - I[spike_mask]) / (self.v_th[spike_mask] - I[spike_mask])) + dt
# Reset voltage of spiking neurons
self.voltage[spike_mask] = 0
# Set refractory time for spiking neurons
self.refractory_time[spike_mask] = self.tau_ref + t_spike
return self.output # Return the output spikes
Show code cell source
import matplotlib.pyplot as plt
t_step = 0.001
neurons = LIFCollection(n=10, dim=1, t_step=t_step)
def compute_response(neuron, inputs, T = 10):
spike_count = np.zeros(len(neuron.output))
for _ in np.arange(0, T, t_step):
output = neuron.step(inputs)
spike_count += output * t_step
return spike_count / T
inputs = np.arange(-1, 1, 0.05)
responses = []
for i in inputs:
response = compute_response(neurons, i)
responses.append(response)
plt.plot(inputs, responses)
plt.show()
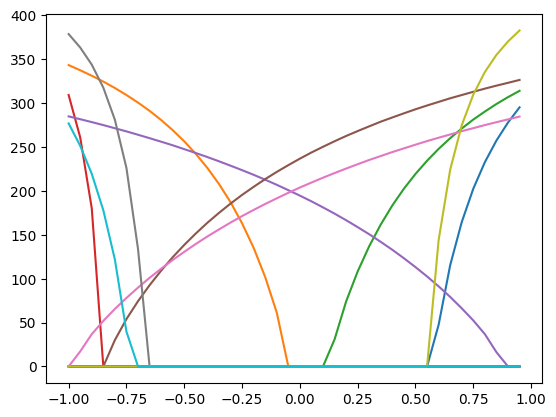
We can do essentially the same thing with our synapses and create a SynapseCollection class to represent many synapses that get updated in parallel.
class SynapseCollection:
def __init__(self, n=1, tau_s=0.05, t_step=0.001):
self.n = n
self.a = np.exp(-t_step / tau_s) # Decay factor for synaptic current
self.b = 1 - self.a # Scale factor for input current
self.voltage = np.zeros(n) # Initial voltage of neurons
def step(self, inputs):
self.voltage = self.a * self.voltage + self.b * inputs
return self.voltage
If we send in a signal (np.sin) and use the decoders from before, we can decode output signals from collections of neurons.
def getDecoders(neurons, minJ=-1, maxJ=1, stepSize=0.01):
def analyticalRate(v_th, tau_ref, tau_rc, I):
if I <= v_th: return 0
else: return 1 / (tau_ref - tau_rc * np.log(1 - v_th/I))
inputs = np.arange(minJ, maxJ, stepSize)
gain_matrix = np.tile(neurons.gain[:, np.newaxis], (1, len(inputs)))
bias_matrix = np.tile(neurons.bias, (1, len(inputs)))
encoders_matrix = np.tile(neurons.encoders, (1, len(inputs)))
I = inputs * gain_matrix * encoders_matrix + bias_matrix
tuningCurves = np.vectorize(analyticalRate)(neurons.v_th[-1], neurons.tau_ref, neurons.tau_rc, I)
A = np.array(tuningCurves)
value = np.expand_dims(inputs, axis=1)
Gamma = A @ A.T + np.identity(len(neurons.output))
GammaInv = np.linalg.inv(Gamma)
Upsilon = A @ value
Phi = GammaInv @ Upsilon
return Phi
Show code cell source
t_step = 0.001
n = 100
neurons = LIFCollection(n=n, t_step=t_step)
synapses = SynapseCollection(n=n, t_step=t_step)
def step(inputs):
neuron_output = neurons.step(inputs)
return synapses.step(neuron_output)
def signal(t):
return np.sin(t)
T = 2*np.pi
t = np.arange(0, T, t_step)
inputs = signal(t)
outputs = []
for i in inputs:
output = step(i)
outputs.append(output)
Phi = getDecoders(neurons)
plt.figure()
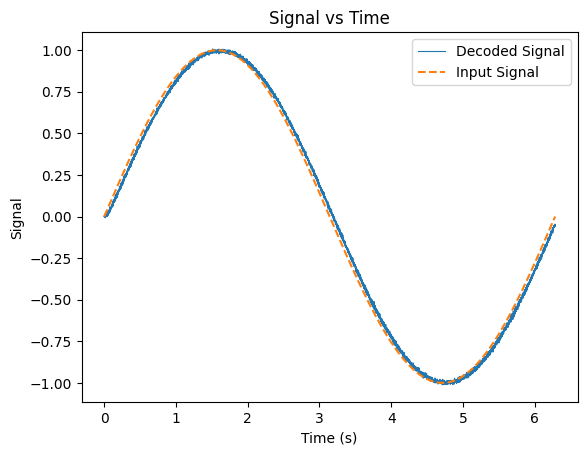
plt.plot(t, outputs @ Phi, linewidth=0.8)
plt.plot(t, inputs, linestyle='--')
plt.xlabel('Time (s)')
plt.ylabel('Signal')
plt.title('Signal vs Time')
plt.legend(['Decoded Signal', 'Input Signal'])
plt.show()
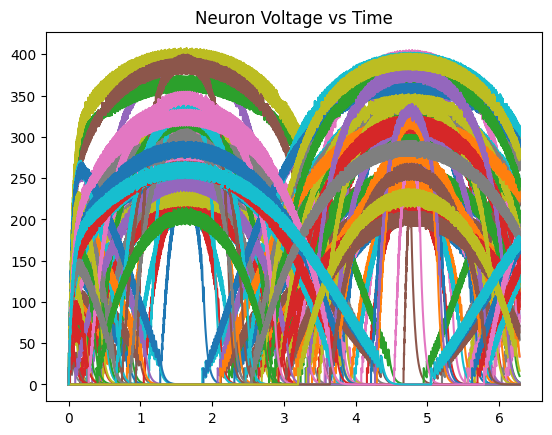
plt.title("Neuron Voltage vs Time")
plt.plot(t, outputs)
plt.show()
Summary#
We can represent (and update) many neurons in parallel using NumPy.