Weights and Connections

When we have multiple groups of neurons, we then would want to connect them. This is done by assigning weights to the connections between the neurons, with the weights being the strength of the connection. For example, a weight of 0 would mean no connection, while a weight of 1 would mean a strong connection.

We can learn connection weights in a variety of ways, as we will go into later.

For now, we will initialize them randomly using np.random.randn(). This will give us a random number from a normal distribution with a mean of 0 and a standard deviation of 1.:

Show code cell source Hide code cell source

import numpy as np

np.random.seed(1) # Set random seed for reproducibility

class LIFCollection:
    def __init__(self, n=1, dim=1, tau_rc=0.02, tau_ref=0.002, v_th=1, 
                 max_rates=[200, 400], intercept_range=[-1, 1], t_step=0.001, v_init = 0):
        self.n = n
        # Set neuron parameters
        self.dim = dim  # Dimensionality of the input
        self.tau_rc = tau_rc  # Membrane time constant
        self.tau_ref = tau_ref  # Refractory period
        self.v_th = np.ones(n) * v_th  # Threshold voltage for spiking
        self.t_step = t_step  # Time step for simulation
        
        # Initialize state variables
        self.voltage = np.ones(n) * v_init  # Initial voltage of neurons
        self.refractory_time = np.zeros(n)  # Time remaining in refractory period
        self.output = np.zeros(n)  # Output spikes

        # Generate random max rates and intercepts within the given range
        max_rates_tensor = np.random.uniform(max_rates[0], max_rates[1], n)
        intercepts_tensor = np.random.uniform(intercept_range[0], intercept_range[1], n)

        # Calculate gain and bias for each neuron
        self.gain = self.v_th * (1 - 1 / (1 - np.exp((self.tau_ref - 1/max_rates_tensor) / self.tau_rc))) / (intercepts_tensor - 1)
        self.bias = np.expand_dims(self.v_th - self.gain * intercepts_tensor, axis=1)
        
        # Initialize random encoders
        self.encoders = np.random.randn(n, self.dim)
        self.encoders /= np.linalg.norm(self.encoders, axis=1)[:, np.newaxis]

    def reset(self):
        # Reset the state variables to initial conditions
        self.voltage = np.zeros(self.n)
        self.refractory_time = np.zeros(self.n)
        self.output = np.zeros(self.n)

    def step(self, inputs):
        dt = self.t_step  # Time step

        # Update refractory time
        self.refractory_time -= dt
        delta_t = np.clip(dt - self.refractory_time, 0, dt) # ensure between 0 and dt

        # Calculate input current
        I = np.sum(self.bias + inputs * self.encoders * self.gain[:, np.newaxis], axis=1)

        # Update membrane potential
        self.voltage = I + (self.voltage - I) * np.exp(-delta_t / self.tau_rc)

        # Determine which neurons spike
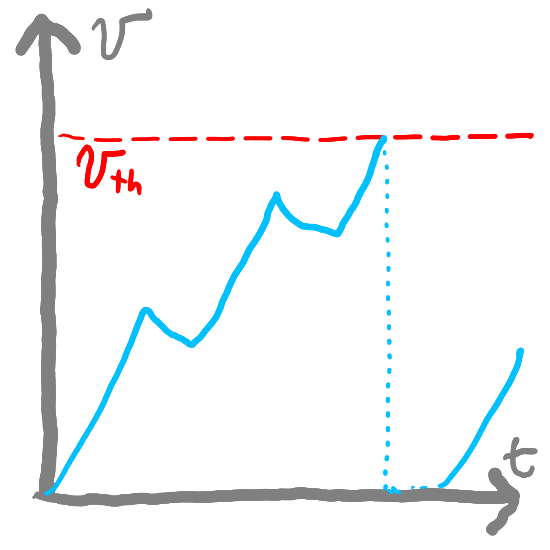
        spike_mask = self.voltage > self.v_th
        self.output[:] = spike_mask / dt  # Record spikes in output

        # Calculate the time of the spike
        t_spike = self.tau_rc * np.log((self.voltage[spike_mask] - I[spike_mask]) / (self.v_th[spike_mask] - I[spike_mask])) + dt

        # Reset voltage of spiking neurons
        self.voltage[spike_mask] = 0

        # Set refractory time for spiking neurons
        self.refractory_time[spike_mask] = self.tau_ref + t_spike

        return self.output  # Return the output spikes
    
class SynapseCollection:
    def __init__(self, n=1, tau_s=0.05, t_step=0.001):
        self.n = n
        self.a = np.exp(-t_step / tau_s)  # Decay factor for synaptic current
        self.b = 1 - self.a  # Scale factor for input current

        self.voltage = np.zeros(n)  # Initial voltage of neurons
    
    def step(self, inputs):
        self.voltage = self.a * self.voltage + self.b * inputs

        return self.voltage

t_step = 0.001

neurons_a = LIFCollection(n=50, tau_rc=0.02, tau_ref=0.002, t_step=t_step)
synapses_a = SynapseCollection(n=neurons_a.n, tau_s=0.1, t_step=t_step)
neurons_b = LIFCollection(n=40, tau_rc=0.02, tau_ref=0.002, t_step=t_step)
synapses_b = SynapseCollection(n=neurons_b.n, tau_s=0.1, t_step=t_step)

weights = np.random.randn(neurons_a.n, neurons_b.n)

outp = []
def step(inp):
    a  = neurons_a.step(inp)
    b  = synapses_a.step(a)
    bw = b @ weights
    c  = neurons_b.step(bw)
    d  = synapses_b.step(c)
    return (a, b, bw, c, d)

T = 10

times = np.arange(0, T, t_step)
def inp(t):
    return np.sin(t)

for t in times:
    outp.append(step(inp(t)))